|
CONVERTING BETWEEN VALUES You may be asked, for example, how many Mi are in a Ti. You don’t need to learn all of the different numbers, just remember the patterns and the rule for dividing numbers with powers:
numbers with powers Ti/Mi = 240/220 = 240-20
Worked Example How many MiB are in a TiB?
Step 1: write down the values for each.
Mib=220 Tib=240
Step 2: work out the difference in powers. Subtract the smaller power (20) from the larger power (40) to get the new power. 40 – 20 = 20 The answer is 2 to the power of the difference in powers, 20. 220 = 1 048 576
How many MB are in 2 GB? Step 1: write down the values for each.
MB=106 GB=109
Step 2: work out the difference in powers. 9 – 6 = 3, so 103 = 1000 Step 3: you need 2 GB, so multiply by 2. 1000 × 2 = 2000 You can also give answer in the form of 2 x103
0 Comments
Binary prefixes
Different quantities of bits can be described with specific names and prefixes. You should know quite a few of these terms, but you also need to know what they represent. ■ At the very basic level you have bits, nibbles and bytes. ■ A bit is just 1 binary digit, e.g. 1 or 0. ■ A nibble is 4 bits, e.g. 0110 or 1101. ■ A byte is 8 bits (or 2 nibbles), e.g. 10101101 or 01011011.After a byte you start recording the number of bits in powers of 10.
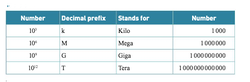
The binary prefix for 210 is Ki and it is called kibi.
the binary prefix for 220 is Mi and stand for Mebi
The binary prefix for 230 is Gi and stand for Gibi
The binary prefix for 240is Ti and stand for Tebi
These are called prefixes because they will all come before what they represent, which is
the number of bytes:
kibibytes= 210 =1024 bytes
mebibytes= 220=1048576 bytes
gigibytes=230=1073741824 bytes
tebibytes=240=1099511627766 bytes
Converting a base 10 to a base 2 or base 16 number
Using division, you can convert a base 10 (decimal) to both base 2 (binary) and base 16 (hexadecimal).
Convert 2910 to base 2 (binary).
■ Divide the number by the base you want it in until you get 0. ■ You want base 2 so you divide by 2. Step 1: divide the number by 2. 29 ÷ 2 = 14 r 1 Step 2: take the quotient (the result) and divide it by 2. 14 ÷ 2 = 7 r 0 Step 3: repeat this process until you have 0 — quotient divided by 2. 7 ÷ 2 = 3 r 1 Still not 0? Repeat — quotient divided by 2. 3 ÷ 2 = 1 r 1 Still not 0? Repeat — quotient divided by 2. 1 ÷ 2 = 0 r 1 Make sure you write your remainder, as this will be used to make the answer. Step 4: now you have 0, write all the remainders from the last to the first; 11101.
convert 10010 to binary (base 2)
Step 1: divide 100 by 2. 100 ÷ 2 = 50 r 0 Step 2: divide the quotient by 2. 50 ÷ 2 = 25 r 0 Step 3: repeat until you have 0. 25 ÷ 2 = 12 r 1 12 ÷ 2 = 6 r 0 6 ÷ 2 = 3 r 0 3 ÷ 2 = 1 r 1 1 ÷ 2 = 0 r 1 Continue dividing by 2 until you have 0. Step 4: write all the remainders, from the last to the first, 1100100.
Convert 2910 to base 16 ( hexadecimal)
Step 1: divide the number by 16.
29 ÷ 16 = 1 r 13 Step 2: divide the quotient by 16. 1 ÷ 16 = 0 r 1 Step 3: repeat until you have 0. Step 4: write the remainders, from the last to first; 1 13. Step 5: check for numbers over 9. You can’t use the number 13 in hexadecimal. You need to replace it with the appropriate letter, D 1 13 becomes 1D Mathematics For Computer Science - Conversion of binary and hexadecimal numbers to decimal numbers9/2/2020 Worked examples a Convert the binary number 0101 to decimal. Step 1: put the binary number into the table format as shown in Table
Step 2: binary is base 2, so replace the word ‘base’ with 2.
Step 3 calculate each column
Step 4: add the columns together. 0 + 4 + 0 + 1 = 5 Convert the hexadecimal number 1D9 to decimal. Step 1: put the hexadecimal number into the table format as shown in Table
Step 2: hexadecimal is base 16, so replace the word ‘base’ with 16.
Step 3: calculate each column, replacing any letters with their numerical equivalent. (D = 13)
Step 4: add the columns together.
256 + 208 + 9 = 473
Each digit in a number can be converted into its decimal (base 10) value using four steps as shown in the Worked examples that follow. Table shows how the digits are presented in table format. In computer science we start counting at 0. The first digit (on the right) is Digit 0 (D0). This is multiplied by its base to the power of 0 (base0) .(D1) is multiplied by its base to the power of 1 (base1) . Digit 2 (D2) is multiplied by its base to the power of 2 (base2).
Multiplying to the power of 2 means the number multiplied by itself, i.e. 42 =4x4 Multiplying to the power of 3 means the number multiplied by itself, i.e. 43 = 4x4x4
‘Number base’ means the number of different symbols that are used. So if you have base
10 (known as decimal, or denary), there are 10 different symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. These symbols are then combined to represent any number, e.g. 12, 99, 386. Binary is base 2 and there are two different symbols: 0 and 1. Hexadecimal is base 16 and there are 16 different symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Letters are used in hexadecimal instead of two-digit numbers. A = 10 B = 11 C = 12 D = 13 E = 14 F = 15 The base of a number can be identified by its subscript: ■ If the subscript is 10, e.g. 910 , this means it is a base 10 number (decimal). ■ If the subscript is 2, e.g. 10112, this means it is a base 2 number (binary). ■ If the subscript is 16, e.g. 28116, this means it is a base 16 number (hexadecimal). Worked examples a) Find A, where A = {x | x ∈ ℤ ∧ x > –3}. Step 1: understand the set comprehension statement. This is asking for all of the values of x, such that x is a member of the set of integers AND x is larger than –3. Step 2: integers are negative and positive whole numbers. Therefore integers larger than –3 are –2, –1, 0, 1, 2, 3, 4 and so on. This set continues infinitely upwards. Step 3: as the set shows a regular sequence, use the … notation to show that the values continue. Therefore, A = {–2, –1, 0, 1, 2, 3, …} b)If A = {7, 8, 9, 10} and B = {5, 6, 7, 8}, find: i A ∪ B The union of two sets includes the elements that are members of either set (or both). Be careful not to repeat any elements. It may be helpful to think of this as joining the sets together and removing any duplicates. A ∪ B = {5, 6, 7, 8, 9, 10} ii A ∩ B The intersection of two sets includes the elements that are members of both sets. A ∩ B = {7, 8} iii A \ B The difference of two sets is simply the elements that are in the first which are not in the second. A \ B = {9, 10} Set operations
The main operations that can be carried out on sets are union, intersection, difference and Cartesian product. ■ The union of sets A and B is the set of all elements that are a member of either or both sets. The symbol ∪ is used to show union. If A = {1, 3, 7, 9} and B = {1, 2, 4, 7} then A ∪ B = {1, 2, 3, 4, 7, 9}. ■ The intersection of sets A and B is the set of all elements that are members of both sets. The symbol ∩ is used to show intersection. Using the same sets for A and B above then A ∩ B = {1, 7}. ■ The difference of sets A and B is the set of all elements that are members of A but not members of B. The symbol \ is used to show difference. Again using the same sets as above, A \ B = {3, 9}. ■ The Cartesian product of two sets is the set of all possible ordered pairs between the two sets. The symbol × (the same symbol that is used for multiplication) is used to denote a cartesian product. For example, if A = {1, 7} and B = {True, False} then A × B = {(1, True), (1, False), (7, True), (7, False)}. Subsets
A subset is defined as a set that is wholly contained within another set. For example, if A = {1, 2, 3, 4} and B = {2, 3} then B is a subset of A. The symbol ⊆ is used to mean subset, so B ⊆ A reads ‘B is a subset of A’. The line in this symbol is reminiscent of an equals sign because a subset can technically have exactly the same elements as the superset. That is, if D = {1, 2, 3, 4} and E = {1, 2, 3, 4}, D = E and D ⊆ E are both true. A proper subset uses the symbol ⊂ and is defined as a subset where at least one element is in the superset that is not in the subset. For example, {1, 2, 3} is a proper subset of ℕ because there is at least one element in ℕ that is not in {1, 2, 3}. |
AuthorLearn the facts about Computer Science. Archives
September 2020
Categories |

 RSS Feed
RSS Feed
